引言

想像一下，你現在要決定「是否要出門打籃球？」
你可能會透過幾個因素來評估，例如：「是否有同伴」、「天氣狀況」、「場地狀況」等等。
所以在你的腦中，可能會經歷像以下這樣的決策過程

今天要不要出門打籃球？
├─ 有球友？
│  ├─ 沒有 → 不出門
│  └─ 有
│     ├─ 下雨？
│     │  ├─ 有
│     │  │  ├─ 有室內球場？ 
│     │  │  │  ├─ 有 → 出門打室內籃球
│     │  │  │  └─ 沒有 → 不出門
│     │  └─ 沒有 → 出門打室外籃球

這樣一步步根據條件來做決策的過程，其實就是 Tree-based model 的核心概念！
而今天的主題，決策樹（Decision Tree） 跟 隨機森林（Random Forest） 的差別就是，你是「自己一個人」做決定 🌳，還是你找「一群朋友」一起幫忙投票決定 🌲🌲🌲

我們前面會先分別介紹這兩種模型的原理，最後會有一個簡單的程式實作哦～

Decision Tree 決策樹

決策樹的分類流程可以畫成像以下這樣的樹狀圖：樹根在上，往下散落出各個葉子。

                   有球友？
                 /       \
               沒有         有
              → 不出門       |
                          下雨？
                        /      \
                      有        沒有
                    /   \      → 出門打室外籃球
            有室內球場？   沒有 
            /      \    → 不出門    
          有       沒有
        → 出門    → 不出門
         打室內籃球

所以問問題是決策流程的關鍵。在每個節點，都會依據對問題的回答走到下一個分支，直到到達最終的葉子節點，就得到分類結果。但決策樹不只是隨便問問題，它會在訓練時會挑選 「最能區分不同類別的特徵」 作為節點的判斷條件。

常用的選擇標準有兩個：

• Entropy（熵）：降低子類別的混亂度
• Gini Impurity（基尼不純度）：最大化子類別的純度

其實他們兩個的訴求是差不多的，都是希望分類後的子類別裡可以越相近越好。只是解釋的角度不同而已～

Random Forest 隨機森林

由於單棵決策樹比較容易會出錯，尤其是當資料類別不太平衡的時候，就有可能做出較偏差的判斷。為了解決這個問題，隨機森林的概念就是用多棵樹一起做決策，然後再投票做出最終決定。當中會有幾個重要的步驟：

1. 隨機抽樣資料（Bootstrap）
從原始資料集中隨機抽取多個子集。抽完後會放回，也就是允許多個子集重複抽到一樣的資料。每個子集會訓練一棵決策樹。
2. 隨機選擇特徵（Feature Bagging）
每棵樹在每個節點分裂時，不是看所有特徵，而是隨機挑選一部分特徵來做判斷。這樣每棵樹在分類時所看的特徵都不一樣，可以讓決策更「多樣化」。
3. 投票決策（Voting）
所有決策樹各自做出判斷後，最後像是投票一樣，由多數決定最終結果。

程式實作

1. 前置預備（詳細步驟分解可以參考前一篇 Naive Bayes）

• 讀取資料：kaggle 的 IMDb 50K Cleaned Movie Reviews
• 資料劃分：訓練集跟測試集切分為 8:2
• 特徵轉換：文字轉為 TF-IDF 向量

import kagglehub
import pandas as pd
import os
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer

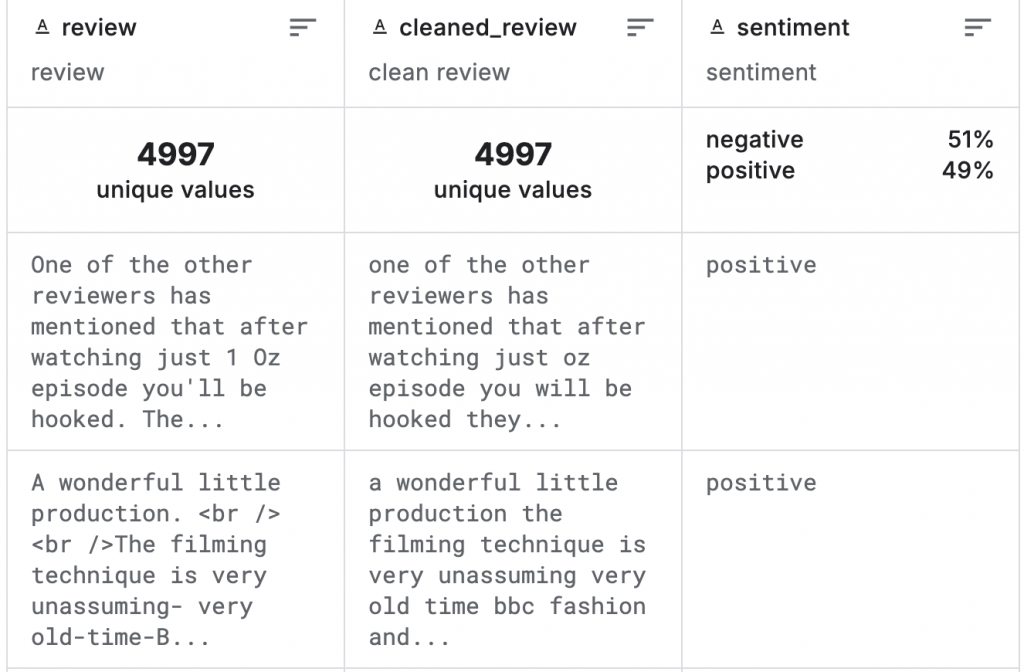
# 讀取資料
path = kagglehub.dataset_download("ibrahimqasimi/imdb-50k-cleaned-movie-reviews")
csv_path = os.path.join(path, "IMDB_cleaned.csv")  
df = pd.read_csv(csv_path)

# 資料劃分
X = df["cleaned_review"]
y = df["sentiment"]

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

# 特徵轉換
vectorizer = TfidfVectorizer(stop_words="english", max_features=5000)
X_train_vec = vectorizer.fit_transform(X_train)
X_test_vec = vectorizer.transform(X_test)

2. Decision Tree

from sklearn.tree import DecisionTreeClassifier

# 建立模型
DT_model = DecisionTreeClassifier(random_state=42)
DT_model.fit(X_train_vec, y_train)
y_pred = DT_model.predict(X_test_vec)

# 評估
print("=== Decision Tree ===")
print("Accuracy:", f"{accuracy_score(y_test, y_pred):.3f}")
print("Precision:", f"{precision_score(y_test, y_pred, pos_label='positive'):.3f}")
print("Recall:", f"{recall_score(y_test, y_pred, pos_label='positive'):.3f}")
print("F1 Score:", f"{f1_score(y_test, y_pred, pos_label='positive'):.3f}")

# 混淆矩陣
cm = confusion_matrix(y_test, y_pred, labels=["positive", "negative"])
plt.figure(figsize=(5,4))
sns.heatmap(cm, annot=True, fmt="d", cmap="Greens", alpha=0.5,
            xticklabels=["positive", "negative"],
            yticklabels=["positive", "negative"])
plt.xlabel("Predicted")
plt.ylabel("Actual")
plt.title("Confusion Matrix - Decision Tree")
plt.show()

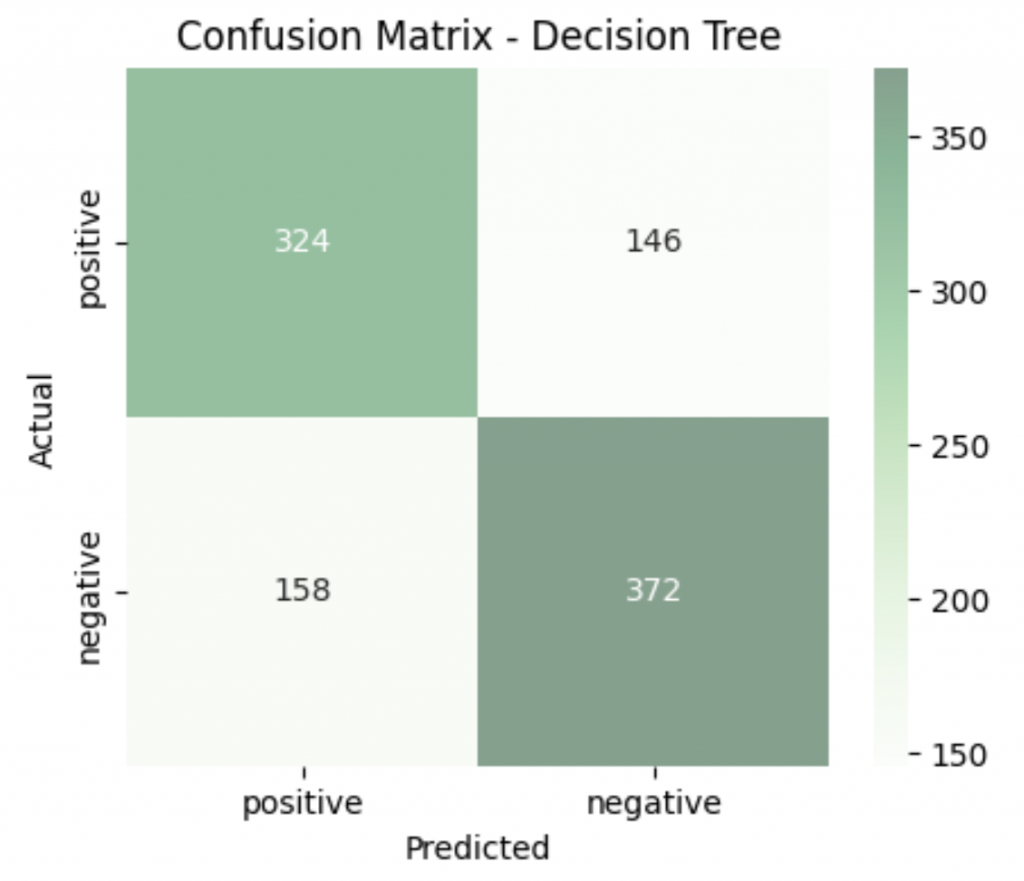
=== Decision Tree ===
Accuracy: 0.696
Precision: 0.672
Recall: 0.689
F1 Score: 0.681

分類報告:
               precision    recall  f1-score   support

    negative       0.72      0.70      0.71       530
    positive       0.67      0.69      0.68       470

    accuracy                           0.70      1000
   macro avg       0.70      0.70      0.70      1000
weighted avg       0.70      0.70      0.70      1000

3. Random Forest

n_estimators：決策樹的棵數

from sklearn.ensemble import RandomForestClassifier

# 建立模型
RF_model = RandomForestClassifier(n_estimators=100, random_state=42)
RF_model.fit(X_train_vec, y_train)
y_pred = RF_model.predict(X_test_vec)

# 評估
print("=== Random Forest ===")
print("Accuracy:", f"{accuracy_score(y_test, y_pred):.3f}")
print("Precision:", f"{precision_score(y_test, y_pred, pos_label='positive'):.3f}")
print("Recall:", f"{recall_score(y_test, y_pred, pos_label='positive'):.3f}")
print("F1 Score:", f"{f1_score(y_test, y_pred, pos_label='positive'):.3f}")

# 混淆矩陣
cm = confusion_matrix(y_test, y_pred, labels=["positive", "negative"])
plt.figure(figsize=(5,4))
sns.heatmap(cm, annot=True, fmt="d", cmap="Greens",
            xticklabels=["positive", "negative"],
            yticklabels=["positive", "negative"])
plt.xlabel("Predicted")
plt.ylabel("Actual")
plt.title("Confusion Matrix - Random Forest")
plt.show()

=== Random Forest ===
Accuracy: 0.819
Precision: 0.818
Recall: 0.791
F1 Score: 0.804

分類報告:
               precision    recall  f1-score   support

    negative       0.82      0.84      0.83       530
    positive       0.82      0.79      0.80       470

    accuracy                           0.82      1000
   macro avg       0.82      0.82      0.82      1000
weighted avg       0.82      0.82      0.82      1000

結語

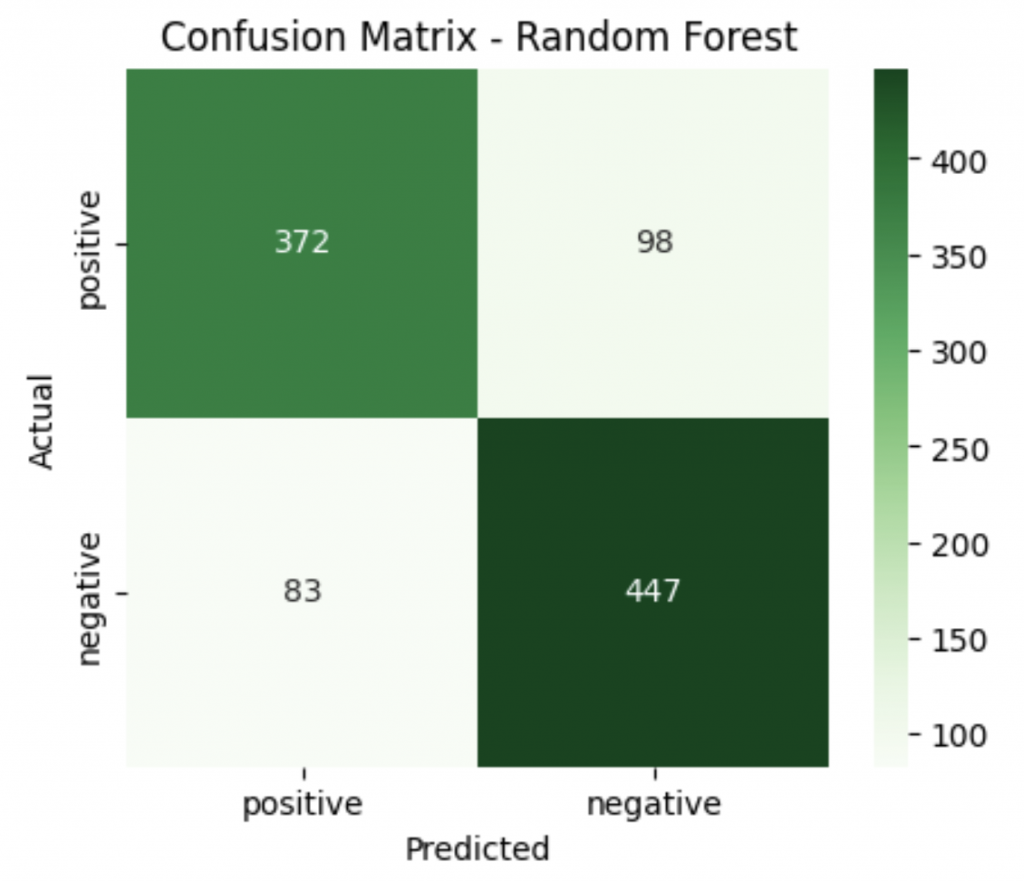
總結一下，今天我們先了解到 Tree-based model 是用「一步一步問問題」來分類的模型。從 決策樹 到 隨機森林 也可以發現，後者以「團體多數決」的方式，表現是會比「單一的決策樹」更好。

那介紹完經典的樹模型，接下來我們要看看另外一個分類的思路，就是直接用「數學方程式」來畫出一條分界線！

明後天我們會介紹 羅吉斯回歸（Logistic Regression） 和 支持向量機（Support Vector Machine），來看看這兩種模型又是如何做分類的吧～～

References

• [資料分析&機器學習] 第3.5講 : 決策樹(Decision Tree)以及隨機森林(Random Forest)介紹
• 隨機森林(Random Forest)的底層概念、操作細節，與推薦相關資源